Building Recursive Descent Parsers: The Definitive Guide

Parsers are programs that help process text. Compilers and interpreters use parsers to analyze programs before processing them further, and parsers for formats like JSON and YAML process text into the programming language’s native data structures.

In this article, we’re going to look at how to build “recursive descent parsers”. Recursive descent parsers are a simple but powerful way of building parsers — for each “entity” in the text that you want to process, you define a function.

First, we are going to look at some of the theory underlying parsing. Then, we using Python, we’re going to build a calculator and a JSON parser that supports comments, trailing commas and unquoted strings. Finally, we’re going to discuss how you can build parsers for other kinds of languages that behave differently than the aforementioned examples.

If you’re already familiar with the theory, you can directly skip to the parts where we build the parser.

How does parsing work?

In order to process a piece of text, a program performs three tasks. In a process called “lexing” or “tokenization”, the program goes over characters in the text, and extracts logical groups called “tokens”. For example, in an expression such as “3 + 5 – 10”, a program to process arithmetic expressions could extract the following tokens:

[{ "Type": "Number"  , "Text": "3"  },
 { "Type": "Operator", "Text": "+"  },
 { "Type": "Number"  , "Text": "5"  },
 { "Type": "Operator", "Text": "-"  },
 { "Type": "Number"  , "Text": "10" }]

The program then uses rules to identify meaningful sequences of tokens, and this is called “parsing”. The rules used to make this happen are called “grammars” — much in the same way that words of a natural language like English are strung together into meaningful sequences using English grammar. Individual rules of a grammar are called “productions”.

Imagine we’re building a program to process math expressions, and we’re interested only in addition and subtraction. An expression must have a number (such as “3”), followed by any number of operators and numbers (such as “+ 5” ). The parsing rule can be visualized like so:

 

The indicates that the group may repeat any number of times (including zero).

Finally, the program takes a set of actions for a grammar rule. For example, after parsing, our math program would need to calculate the value of the expression.

Although we’ve described these as separate steps, a program can perform all of these at once. Doing all the steps at once carries a few advantages, and this is the approach we’re going to take in this article.

Writing production rules

Through the rest of this article, we’re going to use production rules to visualize grammars. Therefore, we’ve explained how we write the production rules throughout this article. If you’ve previously gone through a textbook on parsing, the notation we’ve used here is a bit different.

Earlier, we’ve seen an example of a simple production. When the grammar rule contains a token’s name, and the token is fairly simple, it’s common to write the token’s text in the grammar. If we consider the previous example, yields a + or a -, so we could rewrite the rule like so:

 

We’ve also seen how we can use to indicate that something repeats any number of times. Similarly, a indicates that something repeats, but it should occur at least once. A indicates something that’s optional.

As an example, suppose we’re building a parser to process a list of conditions, like “x > 10 and y > 30”. Assume that the and is optional, so we could rewrite this condition as “x > 10 y > 30”. You could design a grammar for the above like so:

When there are multiple alternatives, the order of alternatives matter. For a rule like , we should try matching a “+” first, and then a “-“. Although in this trivial example it might seem that order does not matter, we’re going to see examples later on where order becomes important.

Finally, a production rule only focuses on tokens and other grammar symbols — it ignores whitespaces and comments.

Considerations when building parsers

Previously, we’ve seen a few simple grammars. However, when trying to parse something more complex, a number of issues can come up. We’re going to discuss them here.

Handling precedence in grammars

Previously, we’ve seen a grammar that can handle a math expression consisting of additions and subtractions. Unfortunately, you can’t extend the same grammar for multiplications (and divisions), since those operations have higher precedence than additions (and subtractions).

In order to handle this scenario, we must design our grammar so that the parser defers any additions, but performs multiplications as soon as it is encountered. To achieve this, we split the grammar into two separate rules, as shown below:

Let us take an expression (such as “3 + 2 * 5”) to ensure that this really works. We’ll assume that once our parser has finished matching a grammar rule, it automatically calculates the expression. We’ll also use underlined text to indicate what the parser is looking for. In addition, we’ve also omitted the quotes for clarity.

When 2 * 5 is parsed, the parser immediately returns the result of 10. This result is received at the step, and the addition is performed at the end, yielding 13 as the result.

In summary, you should arrange your rules so that operators with the lowest precedence are at the top, while the ones with highest precedence are at the bottom.

Avoiding left recursion

Earlier, we have mentioned that a recursive descent parser consists of functions that process “entities” in the text. Now that we know about tokens and production rules, let us redefine this a bit more formally: each function in the parser extracts a token, or implements the logic of a production rule.

Let us take a simple grammar, such as to see what this really means. If you wrote the pseudocode for this grammar, it would look something like this:

def expression():
    first_number = number()
    read('+')
    second_number = number()
    # process these two numbers, e.g. adding them

Next, consider a grammar that parses a list of comma separated numbers. You’d generally write it as:

Now, imagine that for some reason, you wanted to avoid the wildcard and rewrite it like so:

This grammar is theoretically correct — it either picks a single number from the text, or it expands to a list with a number at the end. The second list, in turn, can expand to another number or a list, until parser finishes through the text.

However, there’s a problem with this approach — you’d enter an infinite recursion! If you try calling the list() function once, you end up calling it again, and so on. You might think that rewriting the grammar as might help. However, if you tried writing a function, you’d read a single number and quit parsing. The number you read might be part of a list like “2, 4, 6” and you won’t be able to read the other numbers.

When dealing with parsing, this is called left recursion. The case that we saw above involves “direct left recursion”, but there’s also “indirect left recursion”, where A calls B, B calls A and so on. In either case, you should rewrite the grammar in another way to avoid this issue.

Avoiding backtracking

Suppose, you’re trying to build a parser that parses an operation of two numbers, such as “2 + 4”, and wrote a grammar in this way:

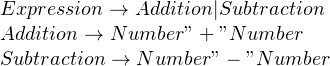
This grammar is correct, and it will also behave in the way you expect and produce correct results. However, this grammar is not what you’d want to use.

To see why this is the case, consider the input string “5 – 2”. We’ll first go with the addition rule, and parse a number. Then, we’d expect a “+” but when reading the string, we’ll get a “-” which means we have to backtrack and apply the subtraction rule. In doing so, we’ve wasted time and CPU cycles on parsing a number, only to discard it and parse it again as part of the subtraction rule.

Additionally, when building parsers that directly work off of data streams, like a network socket, rewinding the stream is often not an option. In this article, we’ll only deal with parsers that have all of the text in memory. Nevertheless, it’s a good practice to avoid backtracking and to do so, you should factor out the common parts from the left. This is how our rule would look after factoring:

The factoring step is complete and will avoid backtracking. However, for aesthetic reasons, we’ll just write it as:

Building a base for the Recursive Descent Parser in Python

Now that we’ve discussed the various considerations for parsing, we’ll build out the calculator and JSON parser. However, before we do that, we’ll write a base “Parser” class that has some methods for common functions, such as recognizing characters and handling errors.

This section might seem a bit too long, but it’s well worth the patience. Once you complete this section, you’ll have all the tooling to build complex parsers with very little code required to recognize tokens and implement production rules.

The exception class

Since this is the easiest task by far, so we’ll tackle this first. We’ll define our own exception class named ParseError like so:

class ParseError(Exception):
    def __init__(self, pos, msg, *args):
        self.pos = pos
        self.msg = msg
        self.args = args

    def __str__(self):
        return '%s at position %s' % (self.msg % self.args, self.pos)

The class accepts the text position where the error occurred, an error message (as a format string), and the arguments to the format string. Let’s see of how you might use this exception type:

e = ParseError(13, 'Expected "{" but found "%s"', "[")

When you try printing the exception, you’ll get a formatted message like this:

Expected "{" but found "[" at position 13

Notice that we haven’t used a % symbol within the format string and its arguments (such as '"Expected "{" but found "%s"' % "["). This is handled in the __str__ method of the class, where we’ve formatted self.msg with elements in self.pos.

Now, you might ask, why do we want to format it in the __str__ method, instead of writing it with a %? It turns out that using the % operator to format a string takes up quite a bit of time. When parsing a string, there’ll be many exceptions raised as the parser tries to apply various rules. Hence, we’ve deferred the string formatting to when it’s really needed.

The base Parser class

Now that we have an error class in place, the next step is to write the parser class. We’ll define it as follows:

class Parser:
    def __init__(self):
        self.cache = {}

    def parse(self, text):
        self.text = text
        self.pos = -1
        self.len = len(text) - 1
        rv = self.start()
        self.assert_end()
        return rv

Here, you’ll notice a cache member in the __init__ method — we’ll get back to why this is needed when we discuss recognizing characters.

The parse method is fairly simple — first, it stores the string. Since we haven’t scanned any part of the string yet, we’ll set the position to -1. Also, we’ll store the maximum index of the string in self.len. (The maximum index is always one less than the length of the string.)

Next, we’ll start parsing the string and check if we’ve reached the end of the string. This is to ensure that our parser was able to process the entire text without anything left at the end. After this, we return the result.

The assert_end method is simple: we’ll check if the current position is less than the maximum index. Bear in mind that these methods are inside the class, although we’ve omitted the indentation for simplicity.

def assert_end(self):
    if self.pos < self.len:
        raise ParseError(
            self.pos + 1,
            'Expected end of string but got %s',
            self.text[self.pos + 1]
        )

Throughout our parser, we’ll be looking at the character that is one more than the current index (self.pos). To see why this is the case, consider that we start out with self.pos = -1, so we’d be looking at the index 0. Once we’ve recognized a character successfully, self.pos goes to 0 and we’d look at the character at index 1, and so on. This is why the error uses self.pos + 1.

With most languages, whitespace between tokens can be safely discarded. Therefore, it seems logical to include a method that checks if the next character is a whitespace character, and if so, “discards” it by advancing to the next position.

def eat_whitespace(self):
    while self.pos < self.len and self.text[self.pos + 1] in " \f\v\r\t\n":
        self.pos += 1

Processing character ranges

Now, we’ll write a function to help us recognize characters in the text. Before we do that though, we’ll consider our function from a user’s perspective — we’ll give it a set of characters to match from the text. For example, if you wanted to recognize an alphabet or underscore, you might write something like:

self.char('A-Za-z_')

We’ll give the char method containing a list of characters or ranges (such as A-Z in the above example). Ranges are denoted through two characters separated by a -. The first character has a numerically smaller value than the one on the right.

Now, if the character at self.text[self.pos + 1] matches something in the argument of self.char, we’ll return it. Otherwise, we’ll raise an exception.

Internally, we’ll process the string into something that’s easier to handle — a list with separate characters or ranges such as ['A-Z', 'a-z', '_']. So, we’ll write a function to split the ranges:

def split_char_ranges(self, chars):
    try:
        return self.cache[chars]
    except KeyError:
        pass

    rv = []
    index = 0
    length = len(chars)

    while index < length:
        if index + 2 < length and chars[index + 1] == '-':
            if chars[index] >= chars[index + 2]:
                raise ValueError('Bad character range')

            rv.append(chars[index:index + 3])
            index += 3
        else:
            rv.append(chars[index])
            index += 1

    self.cache[chars] = rv
    return rv

Here, we loop through the chars string, looking for a - followed by another character. If this condition matches and the first character is smaller than the last, we add the entire range (such as A-Z) to the list rv. Otherwise, we add the character at chars[index] to rv.

Then, we add the list in rv it to the cache. If we see this string a second time, we’ll return it from the cache using the try ... except KeyError: ... block at the top.

Admittedly, we could have just provided a list like ['A-Z', 'a-z', '_'] to the char method. However, in our opinion, doing it in this way makes calls to char() look a bit cleaner.

Extracting characters from the text

Now that we have a method that gives a list containing ranges and characters, we can write our function to extract a character from the text. Here’s the code for the char method:

def char(self, chars=None):
    if self.pos >= self.len:
        raise ParseError(
            self.pos + 1,
            'Expected %s but got end of string',
            'character' if chars is None else '[%s]' % chars
        )

    next_char = self.text[self.pos + 1]
    if chars == None:
        self.pos += 1
        return next_char

    for char_range in self.split_char_ranges(chars):
        if len(char_range) == 1:
            if next_char == char_range:
                self.pos += 1
                return next_char
        elif char_range[0] <= next_char <= char_range[2]:
            self.pos += 1
            return next_char

    raise ParseError(
        self.pos + 1,
        'Expected %s but got %s',
        'character' if chars is None else '[%s]' % chars,
        next_char
    )

Let us first focus on the argument chars=None. This allows you to call self.char() without giving it a set of characters. This is useful when you want to simply extract a character without restricting it to a specific set. Otherwise, you can call it with a range of characters, as we’ve seen in the previous section.

This function is fairly straightforward — first, we check if we’ve run out of text. Then, we pick the next character and check if chars is None, in which case we can increment the position and return the character immediately.

However, if there are a set of characters in chars, we split it into a list of individual characters and ranges, such as ['A-Z', 'a-z', '_']. In this list, a string of length 1 is a character, and anything else is a range. It checks if the next character matches the character or the range, and if it does, we return it. If we failed to match it against anything, it exits the loop which raises ParseError, stating that we couldn’t get the expected character.

The 'character' if chars is None else '[%s]' % chars is just a way of providing a more readable exception. If chars is None,  the exception’s message would read Expected character but got ..., but if char was set to something like A-Za-z_, we’d get Expected [A-Za-z_] but got ....

Later on, we’ll see how to use this function to recognize tokens.

Extracting keywords and symbols

Apart from extracting individual characters, recognizing keywords is a common task when building a parser. We’re using “keywords” to loosely refer to any contiguous string that is it’s “own entity”, and may have whitespace before and after it. For example, in JSON { could be a keyword, and in a programming language if, else could be a keyword, and so on.

This is the code for recognizing keywords:

def keyword(self, *keywords):
    self.eat_whitespace()
    if self.pos >= self.len:
        raise ParseError(
            self.pos + 1,
            'Expected %s but got end of string',
            ','.join(keywords)
        )

    for keyword in keywords:
        low = self.pos + 1
        high = low + len(keyword)

        if self.text[low:high] == keyword:
            self.pos += len(keyword)
            self.eat_whitespace()
            return keyword

    raise ParseError(
        self.pos + 1,
        'Expected %s but got %s',
        ','.join(keywords),
        self.text[self.pos + 1],
    )

This method takes keywords, such as self.keyword('if', 'and', 'or'). The method strips whitespace and then checks if we’ve run out of text to parse. It then iterates through each keyword, checking if the keyword exists in the text. If it does find something, we’ll strip the whitespace following the keyword, and then return the keyword.

However, if it doesn’t find something, it exits the loop which raises ParseError, stating that the keywords couldn’t be found.

A helper for matching multiple productions

In the previous sections, you’ve noticed that we use exceptions to report errors. We also know that to write a recursive descent parser, you write functions that recognize a token or a production rule. Now, imagine that you wanted to parse a simple text, where you expect a number or a word. The production rule might look like:

We’ll also assume that the text contains a word. When the parser tries to look for a digit (perhaps by using char() ), it won’t find it, and this causes it to raise an exception. In addition, you have to strip the whitespace before and after matching a production rule. So, the code for item() might look like this:

def item(self):
	self.eat_whitespace()
	try:
		rv = self.number()
	except ParseError:
		rv = self.word()
	self.eat_whitespace()
	return rv

This already looks like a lot to implement a simple rule! Imagine what it would be like to implement a complex rule — you’d have to use try...except blocks all over the place.

So, we’ll write a match() function that’ll strip the whitespace and try to match multiple rules. The function is as follows:

def match(self, *rules):
    self.eat_whitespace()
    last_error_pos = -1
    last_exception = None
    last_error_rules = []

    for rule in rules:
        initial_pos = self.pos
        try:
            rv = getattr(self, rule)()
            self.eat_whitespace()
            return rv
        except ParseError as e:
            self.pos = initial_pos

            if e.pos > last_error_pos:
                last_exception = e
                last_error_pos = e.pos
                last_error_rules.clear()
                last_error_rules.append(rule)
            elif e.pos == last_error_pos:
                last_error_rules.append(rule)

    if len(last_error_rules) == 1:
        raise last_exception
    else:
        raise ParseError(
            last_error_pos,
            'Expected %s but got %s',
            ','.join(last_error_rules),
            self.text[last_error_pos]
        )

Before we discuss how it works, let’s see how simple it is to rewrite our previous example using match():

def item(self):
    return self.match('number', 'word')

So, how does that work? match() takes a method name to run (such as number or word in the above example). First, it gets rid of the whitespace at the beginning. Then, it iterates over all the method names and fetches each method using its name via getattr(). It then tries to invoke the method, and if all goes well, it’ll strip whitespace after the text as well. Finally, it returns the value that it received by calling the method

However, if there’s an error, it resets self.pos to the value that was there before trying to match a rule. Then, it tries to select a good error message by using the following rules:

• When matching multiple rules, many of them might generate an error. The error that was generated after parsing most of the text is probably the error message we want.

To see why this is the case, consider the string “abc1”. Trying to call number() would fail at position 0, whereas word() would fail at position 2. Looking at the string, it’s quite likely that the user wanted to enter a word, but made a typo.

• If two or more erroring rules end up in a “tie”, we prefer to tell the user about all the rules which failed.

The last_error_pos and last_exception keeps track of the last error’s position and exception respectively. In addition, we maintain a list last_error_rules so that in case of a tie, we can tell the user about all the rules we tried to match.

In the except ParseError block, we compare the last error’s position and the current error. If the current error is equal, we consider it a tie and append to the list. Otherwise, we update the error position, exception and list of errored rules.

In the end, we check how many rules failed. If there’s only one, last_exception would have the best error message. Otherwise, it’s a tie, and we’ll let the user know with a message like Expected number,word but found ....

Looking ahead at what’s next – helper functions

At this point, we have all the necessary things in our parser, and all failures throw exceptions. However, sometimes we want to only match a character, keyword or rule if it’s there, without the inconvenience of handling exceptions.

We’ll introduce three small helpers to do just that. In the case of an exception when looking for stuff, these will return None:

def maybe_char(self, chars=None):
    try:
        return self.char(chars)
    except ParseError:
        return None

def maybe_match(self, *rules):
    try:
        return self.match(*rules)
    except ParseError:
        return None

def maybe_keyword(self, *keywords):
    try:
        return self.keyword(*keywords)
    except ParseError:
        return None

Using these functions are easy. This is how you might use them:

operator = self.maybe_keyword('+', '-'):
if operator == '+':
    # add two numbers
elif operator == '-':
    # subtract two numbers
else: # operator is None
    # do something else

First parser example: a calculator

Now that we’ve built the foundation for writing a parser, we’ll build our first parser. It’ll be able to parse mathematical expressions with additions, subtractions, multiplications, divisions, and also handle parenthesized expressions like “(2 + 3) * 5”.

We will begin by visualizing the grammar in the form of production rules.

Production rules for the calculator grammar

We’ve previously seen a grammar to handle everything except for parenthesized expressions:

Now, let’s think about how parenthesized expressions fit in to this grammar. When evaluating “(2 + 3) * 5”, we’d have to calculate “(2 + 3)” and reduce it to a number. Which means that in the above grammar, the term “Number” can either refer to a parenthesized expression, or something that’s really a number, like “5”.

So, we’ll tweak our rules to accommodate both. In the rule for “Term”, we’ll replace “Number” for a more appropriate term like “Factor”. “Factor” can then either refer to a parenthesized expression, or a “Number”. The modified grammar looks like this:

With that out of the way, let’s implement the production rules!

Implementing the parser

We’ll implement our Calculator parser by extending the base Parser class. We begin defining the class like so:

class CalcParser(Parser):
    def start(self):
        return self.expression()

Previously, when implementing the base parser class, we had a start() method to start parsing. We’ll simply call the expression() method here, which we’ll define as below:

def expression(self):
    rv = self.match('term')
    while True:
        op = self.maybe_keyword('+', '-')
        if op is None:
            break

        term = self.match('term')
        if op == '+':
            rv += term
        else:
            rv -= term

    return rv

The grammar rule for . So, we start by reading a term from the text. We then set up an infinite loop, and look for a “+” or “-“. If we don’t find either, this means that we’ve finished reading through the list of additional terms as given by , so we can break out of the loop.

Otherwise, we read another term from the text. Then, depending upon the operator, we either add or subtract it from the initial value. We continue with this process until we fail to get a “+” or “-“, and return the value at the end.

We’ll implement term() in the same way:

def term(self):
    rv = self.match('factor')
    while True:
        op = self.maybe_keyword('*', '/')
        if op is None:
            break

        term = self.match('factor')
        if op == '*':
            rv *= term
        else:
            rv /= term

    return rv

Next, we’ll implement “Factor”. We’ll try to read a left parenthesis first, which means that there’s a parenthesized expression. If we do find a parenthesis, we read an expression and the closing parenthesis, and return the value of the expression. Otherwise, we simply read and return a number.

def factor(self):
    if self.maybe_keyword('('):
        rv = self.match('expression')
        self.keyword(')')

        return rv

    return self.match('number')

In the next section, we’re going to make our parser recognize a number.

Recognizing numbers

In order to recognize a number, we need to look at the individual characters in our text. Numbers consist of one or more digits, optionally followed by a decimal part. The decimal part has a period (.), and followed by at least one digit. In addition, numbers may have a sign such as “+” or “-” before them, such as “-124.33”.

We’ll implement the number() method like so:

def number(self):
    chars = []

    sign = self.maybe_keyword('+', '-')
    if sign is not None:
        chars.append(sign)

    chars.append(self.char('0-9'))

    while True:
        char = self.maybe_char('0-9')
        if char is None:
            break

        chars.append(char)

    if self.maybe_char('.'):
        chars.append('.')
        chars.append(self.char('0-9'))

        while True:
            char = self.maybe_char('0-9')
            if char is None:
                break

            chars.append(char)

    rv = float(''.join(chars))
    return rv

Although the function is long, it’s fairly simple. We have a chars list in which we put the characters of the number. First, we look at any “+” or “-” symbols that may be present before the number. If it is present, we add it to the list. Then, we look for the first mandatory digit of the number and continue looking for more digits using the maybe_char() method. Once we get None through maybe_char, we know that we’re past the set of digits, and terminate the loop.

Similarly, we look for the decimal part and its digits. Finally, we convert all the characters into a string, which in turn, we convert to a floating point number.

An interface for our parser

We’re done building our parser. As a final step, we’ll add a little bit of code in the global scope that’ll allow us to enter expressions and see results:

if __name__ == '__main__':
    parser = CalcParser()

    while True:
        try:
            print(parser.parse(input('> ')))
        except KeyboardInterrupt:
            print()
        except (EOFError, SystemExit):
            print()
            break
        except (ParseError, ZeroDivisionError) as e:
            print('Error: %s' % e)

If you’ve followed along so far, congratulations! You have built your first recursive descent parser!

If you’re following along in a local IDE, you can run your code at this point. Alternatively, you can use the playground below to run the parser. You can enter expressions through the “Input” tab below:

You can also find the full code here.

Second parser example: an “extended” JSON parser

JSON is a data interchange format that supports basic data structures like numbers, strings and lists. It’s a very widely used format, although it’s simplicity means that it’s lacking things like comments and strict about the things it accepts. For example, you can’t have a trailing comma in a list or have an explicit “+” in front of a number to indicate its sign.

Since Python already has a JSON module, we’re going to aim for a little higher and build a JSON parser that supports comments, trailing commas and unquoted strings.

Implementing this parser will teach you how to handle comments. It’ll also illustrate how making an easy to use language can make parsing complicated, and how you can deal with such situations.

Before we implement our grammar, let us get a feel for our extended JSON format:

{
	# Comments begin with a '#' and continue till the end of line.

	# You can skip quotes on strings if they don't have hashes,
	# brackets or commas.
	Size: 1.5x,

	# Trailing commas are allowed on lists and maps.
	Things to buy: {
		Eggs : 6,
		Bread: 4,
		Meat : 2,
	},

	# And of course, plain JSON stuff is supported too!
	"Names": ["John", "Mary"],
	"Is the sky blue?": true
}

Production rules for the JSON grammar

Our extended JSON sticks to the same data types that JSON supports. JSON has four primitive data types — null, booleans, numbers and strings, and two complex data types — lists (or arrays), and maps (also called hashes or dictionaries). Lists and hashes look similar to the way they do in Python.

Since JSON data would consist of one of these types, you might write the production rules like so:

Then, you can break up these two types into JSON’s types:

This grammar is fine for parsing regular JSON but needs a bit of tweaking for our case. Since we’re going to support unquoted strings, which means “1.5” (without the quotes) is a number, but “1.5x” (again, without the quotes), is a string. Our current grammar would read the “1.5” from “1.5x”, and then cause an error because “x” wasn’t expected after a number.

This means that first, we’d have to get the full set of unquoted characters. Next, we’ll analyze the characters and determine if it’s a number or a string. So, we’ll combine numbers and unquoted strings into a single category, “Unquoted”. The quoted strings are fine, so we’ll separate them into another category, “QuotedString”. Our modified production rule for “PrimitiveType” now looks like this:

In addition, the order of the rules is important. Since we have unquoted keys, we must first try parsing the text as a null or a boolean. Otherwise, we might end up recognizing “null” or “true” as an unquoted string.

Implementing the parser and dealing comments

To implement the JSON parser, we’ll begin by extending the base parser class like so:

class JSONParser(Parser):
	# ...

We will first tackle the problem of dealing with comments. If you think about it, comments are really similar to whitespace — they occur in the same places where whitespaces can occur, and they can be discarded just like whitespace. So, we’ll reimplement eat_whitespace() to deal with the comments, like so:

def eat_whitespace(self):
    is_processing_comment = False

    while self.pos < self.len:
        char = self.text[self.pos + 1]
        if is_processing_comment:
            if char == '\n':
                is_processing_comment = False
        else:
            if char == '#':
                is_processing_comment = True
            elif char not in ' \f\v\r\t\n':
                break

        self.pos += 1

Here, we need to keep track of whether we’re processing whitespaces or a comment. We loop over the text character-by-character, checking if we have whitespaces or a #. When there’s a #, we update is_processing_comment to True and in the next iterations of the while loop, we can safely discard all characters until we reach the end of the line. However, when processing whitespace characters, we must stop once a non-whitespace character appears.

Next, we’ll implement the production rules and the start() method. The input text will have a JSON type contained in it, so we’ll simply call any_type() in the start() method:

def start(self):
    return self.match('any_type')

def any_type(self):
    return self.match('complex_type', 'primitive_type')

def primitive_type(self):
    return self.match('null', 'boolean', 'quoted_string', 'unquoted')

def complex_type(self):
    return self.match('list', 'map')

Parsing lists and maps

Previously, we’ve seen how to parse comma separated lists. JSON’s lists are just a comma separated list with square brackets tacked onto them, and the list may have zero or more elements. Let’s see how you would implement parsing a list:

def list(self):
    rv = []

    self.keyword('[')
    while True:
        item = self.maybe_match('any_type')
        if item is None:
            break

        rv.append(item)

        if not self.maybe_keyword(','):
            break

    self.keyword(']')
    return rv

We begin by reading off the initial square bracket followed by an item from the list using self.maybe_match('any_type'). If we failed to get an item, this indicates that we’re probably done going through all the items, so we break out of the loop. Otherwise, we add the item to the list. We then try to read a comma from the list, and the absence of a comma also indicates that we’re done with the list.

Similarly, maps are just comma separated lists of “pairs” with braces, where a pair is a string key followed by a colon(:) and a value. Unlike Python’s dicts which can have any “hashable” type as a key (which includes ints and tuples), JSON only supports string keys.

This is how you’d implement the rules for maps and pairs:

def map(self):
    rv = {}

    self.keyword('{')
    while True:
        item = self.maybe_match('pair')
        if item is None:
            break

        rv[item[0]] = item[1]

        if not self.maybe_keyword(','):
            break

    self.keyword('}')
    return rv

def pair(self):
    key = self.match('quoted_string', 'unquoted')

    if type(key) is not str:
        raise ParseError(
            self.pos + 1,
            'Expected string but got number',
            self.text[self.pos + 1]
        )

    self.keyword(':')
    value = self.match('any_type')

    return key, value

In pair(), we try to read a “QuotedString” or “Unquoted” for the key. As we’ve mentioned previously, “Unquoted” can either return a number or a string, so we explicitly check if the key that we’ve read is a string. pair() then returns a tuple with a key and value, and map() calls pair() and adds these to a Python dict.

Recognizing null and boolean

Now that the main parts of our parser are implemented, let us begin by recognizing simple tokens such as null and booleans:

def null(self):
    self.keyword('null')
    return None

def boolean(self):
    boolean = self.keyword('true', 'false')
    return boolean[0] == 't'

Python’s None is the closest analogue to JSON’s null. In the case of booleans, the first characters is sufficient to tell whether it’s true or false, and we return the result of the comparison.

Recognizing unquoted strings and numbers

Before moving on to recognize unquoted strings, let us first define the set of acceptable characters. We’ll leave out anything that’s considered special in such as braces, quotes, colons, hashes (since they are used in comments) and backslashes (because they’re used for escape sequences). We’ll also include spaces and tabs in the acceptable set of characters so that you can write strings like “Things to buy” without using quotes.

So, what are the characters that we want to accept? We can use Python to figure this out:

>>> import string
>>> ''.join(sorted(set(string.printable) - set('{}[]:#"\'\f\v\r\n')))
'\t !$%&()*+,-./0123456789;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ\\^_`abcdefghijklmnopqrstuvwxyz|~'

The next question is, how do you figure out if the text you read is a number or a string? The answer is — we cheat! Since Python’s int() and float() can take a string and return a number, we’ll use them and if those result in a ValueError, we’ll return a string. As for when to use int() or float(), we’ll use a simple rule. If the text contains “E”, “e” or “.”, (for example, “12.3” or “2e10”), we’ll call float(); otherwise, we’ll use int().

Here’s the code:

def unquoted(self):
    acceptable_chars = '0-9A-Za-z \t!$%&()*+./;<=>?^_`|~-'
    number_type = int

    chars = [self.char(acceptable_chars)]

    while True:
        char = self.maybe_char(acceptable_chars)
        if char is None:
            break

        if char in 'Ee.':
            number_type = float

        chars.append(char)

    rv = ''.join(chars).rstrip(' \t')
    try:
        return number_type(rv)
    except ValueError:
        return rv

Since matching rules are handled by match(), this takes care of stripping any initial whitespace before unquoted() can run. In this way, we can be sure that unquoted() won’t return a string consisting of only whitespaces. Any whitespace at the end is stripped off before we parse it as a number or return the string itself.

Recognizing quoted strings

Quoted strings are fairly simple to implement. Most programming languages (including Python) have single and double quotes that behave in the same way, and we’ll implement both of them.

We’ll support the following escape sequences — \b (backspace), \f (line feed), \n (newline), \r (carriage return), \t (tab) and \u(four hexadecimal digits) where those digits are used to represent an Unicode “code point”. For anything else that has a backslash followed by a character, we’ll ignore the backslash. This handles cases like using the backslash to escape itself (\\) or escaping quotes (\").

Here’s the code for it:

def quoted_string(self):
    quote = self.char('"\'')
    chars = []

    escape_sequences = {
        'b': '\b',
        'f': '\f',
        'n': '\n',
        'r': '\r',
        't': '\t'
    }

    while True:
        char = self.char()
        if char == quote:
            break
        elif char == '\\':
            escape = self.char()
            if escape == 'u':
                code_point = []
                for i in range(4):
                    code_point.append(self.char('0-9a-fA-F'))

                chars.append(chr(int(''.join(code_point), 16)))
            else:
                chars.append(escape_sequences.get(char, char))
        else:
            chars.append(char)

    return ''.join(chars)

We first read a quote and then read additional characters in a loop. If this character is the same type of quote as the first character we read, we can stop reading further and return a string by joining the elements of chars.

Otherwise, we check if it’s an escape sequence and handle it in the aforementioned way, and add it to chars. Finally, if it matches neither of them, we treat it as a regular character and add it to our list of characters.

An interface for our JSON parser

To make sure we can interact with our parser, we’ll add a few lines of code that accepts input and parses it as JSON. Again, this code will be in global scope:

if __name__ == '__main__':
    import sys
    from pprint import pprint

    parser = JSONParser()

    try:
        pprint(parser.parse(sys.stdin.read()))
    except ParseError as e:
        print('Error: '+ str(e))

To ensure we can read multiple lines, we have used sys.stdin.read(). If you’re going to run this locally, you can enter text and use Ctrl+D to stop the program from asking for more input. Otherwise, you can use this runnable snippet:

You can find the complete code here.

Building other kinds of parsers

Now that we’ve gone through building two parsers, you might have a fairly good idea of how to roll your own for the task at hand. While every language is unique (and therefore, their parsers), there are some common situations that we haven’t covered. For the sake of brevity, we won’t cover any code in these sections.

Whitespace sensitive languages

Before we begin, let us clarify that we’re not referring to languages that use whitespace-based indentation — we’ll cover them in the next section. Here, we’ll discuss languages where the meaning of things change based on the whitespace you put between elements.

An example of such a language would be where “a=10” is different than “a = 10”. With bash and some other shells, “a=10” sets an environment variable, whereas “a = 10” runs the program “a” with “=” and “10” as command-line arguments. You can even combine the two! Consider this:

a=10 b=20 c = 30

This sets the environment variables “a” and “b” only for the program “c”. The only way to parse such a language is to handle the whitespaces manually, and you’d have to remove all the eat_whitespace() calls in keyword() and match(). This is how you might write the production rules:

 

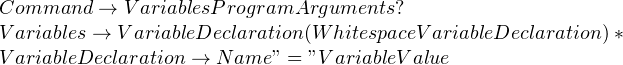
Whitespace based indentation

Languages like C and Javascript use curly braces to indicate the body of loops and if-statements. However, Python uses indentation for the same purpose, which makes parsing tricky.

One of the methods to handle this is to introduce a term such as “INDENT” to keep track of indented statements. To see how this would work, consider the following production rule:

 

After matching a condition, our parser would look for INDENT. Since this is the first time it’s trying to match INDENT, it takes whatever whitespace (except for newlines) that appears along with a non-whitespace character (since that would be part of a statement).

In subsequent iterations, it looks for the same whitespace in the text. If it encounters a different whitespace, it can raise an error. However, if there’s no whitespace at all, it indicates that the “while” loop is finished.

For nested indentations, you’d need to maintain a list of all indentations that you’re currently handling. When the parser handles a new indented block, it should add the new indentation string on the list. You can tell if you’re done parsing the block, by checking that you were able to retrieve less whitespace than you did previously. At this point, you should pop off the last indentation off the list.

If you liked this post, please share it :)